この問題の元ネタは以下の通りです。
rを正の実数とする。xyz空間内の原点O(0,0,0)を中心とする半径1の球をA、点P(r,0,0)を中心とする半径1の球をBとする。球Aと球Bの和集合の体積をVとする。ただし、球Aと球Bの和集合とは、球Aまたは球Bの少なくとも一方に含まれる点全体よりなる立体のことである。
(1) Vをrの関数として表し、そのグラフの概形をかけ。
(2) V=8になるとき,rの値はいくらか。四捨五入して小数第1位まで求めよ。
注意：円周率πは3.14<π<3.15を満たす。
※2004年度 東京大学(理系)前期日程 数学
以下に解説をまじえ解答を示します。
なお問題は微積について学んでいることを前提としているようなので（微積の基礎から説明するのは大変なので）「そういえば習ったな」くらいのひとを想定して記述してます。

部分が解答です。
この問題を解く上で最初に考える（思い浮かべる）ことは、
1.和集合っていうのは和して集めて合わせるからかなり足した感じがする。平たくいえばプログラミング言語のOR演算のことのようだ。
2.点全体よりなる立体という表現は求積法、つまり積分の問題と受け止めるよう示唆していると思われる。
3.問い(1)の関数やグラフは問い(2)のヒントになりそうっぽいから、問い(2)は問い(1)を解くまで忘れてたほうがよいかも。
4.でも問い(2)は円周率がどうとか小数第1位がどうとか言ってるのがヒントっぽい。
(1) Vをrの関数として表し、そのグラフの概形をかけ。

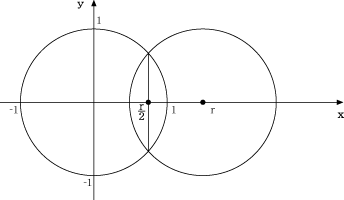
半径が1と書いてあるので、球Aと球Bが重なったり重ならなかったりする状態はそれぞれの球の中心点を結ぶ距離の関係においては2が境となります。なので場合分けをしてそれぞれ考えるという方針で行きます。
rについて、r>2の場合、r=2の場合、0<r<2の場合に分けて考える。

場合分けする意図を分かりやすくするためにz=0の場合(つまりxy空間)でのグラフを描いておきます。後に積分を利用するのでそこでも利用します。
(i) r>2のとき

球Aと球Bは共通部分がないので

V=
4
3
π×
1 3
+
4
3
π×
1 3
=
8
3
π

この部分は積分で求めることも可能ですが、ここでは球の体積を求める公式（身の上に心配あーる3乗）を使っています。なお、球の体積の求めかたはアルキメデスが最初だそうです。
また、関数Vの式にはrが含まれてませんが、r>2という限定条件も関数のうちということにします。
(ii) r=2のとき
球Aと球Bはx=r=2においてx軸上(y=z=0)で点が交わる。

普通に考えると、このそれぞれの球における2点(交点)はxyz空間上同値の点(位置)であり距離(長さ)がないので体積は0です。
が、微積に関する設問のようなので、極限値によって説明したほうが良いようにも感じます。
この点の体積をhとし、交点の点としての性質(距離)を考えると、
V=
8
3
π -
1
2
(
lim h
h→0
) =
8
3
π

重なってる部分の片方（半分）を取り除けば正味の体積が分かるという話ですが、実際に重なっている部分の体積は0です。
これはちょっと定石的な解答ではないような気がするので、r=2については知らないふりをして(i)もしくは(iii)に紛れ込ませたほうがよいかも知れません。つまり、r≧2もしくは0<r≦2として一緒に解答してしまうわけです。
なお、限りなく0に近い距離（や面積、体積）は0であると認めないと、アキレスは亀に追い付かないことになってしまいます。「アキレスが亀に追い付くまでの瞬間には亀はその時間の間に少しだけ先に進んでいる。で、その進んだ分の距離を縮めた瞬間にはさらに少しだけ亀は先に進んでしまっている(以後繰り返し)」というやつです。これをどこまでも繰り返すと距離と時間は限りなく小さくなっていくわけですが、経験的にアキレスは亀に追い付くことが分かるので限りなく0に近い距離は0と等しいと認められて良いのでしょう。とはいえ、どこか騙されてるような話ではあります。
ちなみに、問題には点全体よりなる立体とあります。
日常的な幾何学においては点に距離はなく、よって体積がないので、点全体よりなる立体も、この日本語の文章による脈絡のなかでとらえると体積0となってしまうので、これは点というより空間的要素全体よりなる立体というようなとらえかたをすればよいのかなとも思えますが、多少、曖昧さが残る気がします。しかし、これは微積の問題のようなので点の集合は3次元空間においては体積であると単純に考えて良さそうです。
(iii) 0<r<2のとき
円
x 2
+
y 2
=
1 2
と円
(x-r) 2
+
y 2
=
1 2
をx軸のまわりに回転して球Aと球Bを作ると考える。

円を表す関数は上記の通りなのですがその根拠も含めて書くと大変なので解答としては「そんなの当然」とばかりに公式として書いています。なお、xy面の原点(0,0)を中心として円を描き、円周上の任意の点からx軸(もしくはy軸)に垂直に交わる線と原点(0,0)に交わる線を引き、そこで出来上がる三角形でピタゴラスの定理を当てはめれば、どうして関数が成り立つのか分かりやすいと思います。→参考
この場合、球Aと球Bは直線x=
r
2
を軸に対称であるので
球Aと球Bの和集合の体積Vは
範囲x=-1からx=
r
2
によって限定される 曲線y=
(1-
x 2
)
をx軸のまわりに回転させた回転体の体積を2倍したものであるから
V =2
r
2
-1
π (
(1-
x 2
)
) 2
dx = 2π
r
2
-1
(1-
x 2
)
dx =2π [ x-
x 3
3
]
r
2
-1

回転体の体積の求めかたはyz面で立体をスライスするとどこでも切り口は円になるので、その円の面積(yzの2次元)をx軸方向に積み重ねていけば球の体積(xyzの3次元)になるという考えに基づいています。
積分は次元(次数)を拡大していくものなのですが、その中で∫(インテグラル)記号の右上下に数字が付く（範囲が限定される）積分は定積分といい面積や体積の求積法(微小な要素の集まりとして計算する方法)です。
これらが成り立つ理由については(Δ:デルタとかlimとか∫とか[]など記号を使った数式や図表の表記がたくさん必要で大変なので)省略しますが、興味のあるかたは専門のウェブサイトなどで調べてみて下さい。なお、一般的な解説としては教科書程度のものがそれに相当するようですが、そもそも面積や体積とは何かということについてまで踏み込む場合はルベーグ積分の名のもととなったルベーグの論文「Integrale, longueur, aire」などが参考になるそうです。
V =2π {
r
2
-(-1)-
1
3
(
r 3
8
-
(-1) 3
) } = π ( -
r 3
12
+r+
4
3
)

以上によりVをrの関数として表すことが出来ました。
次に導関数

関数Vにおいてrの変化に係わるVの増減の様子が上の式からでは一見して分かりづらいので関数を微分して調べてみようということです。
V'=
dV
dr
= π ( -
r 2
4
+1 ) =-
1
4
π (
r 2
-4 ) =-
1
4
π (r+2)(r-2)
により関数Vの接線の傾きである微分係数V'は範囲0<r<2において常に0より大きいことから
rが0から2に向かうに従い体積Vは増加して行き、

導関数V'をy、rをxと書き換えると因数分解で解が分かる普通の二次方程式で、範囲0<r<2においてはV'の値は常に0より大きいことが分かります。
また、第2次導関数、
V''=
d 2 V
dr 2
=-
π
2
r <0
により関数Vは上に凸である。

これはグラフ上で関数Vの描くカーブの角度がrの増加に関して「緩→急」カーブなのか「急→緩」カーブなのか調べています。rの値に係わらずV''はマイナスなので「急→緩」カーブであることが分かります。ここで言う「急→緩」カーブというのは下に開いた放物線が描くようなカーブ（の増加部分）です。
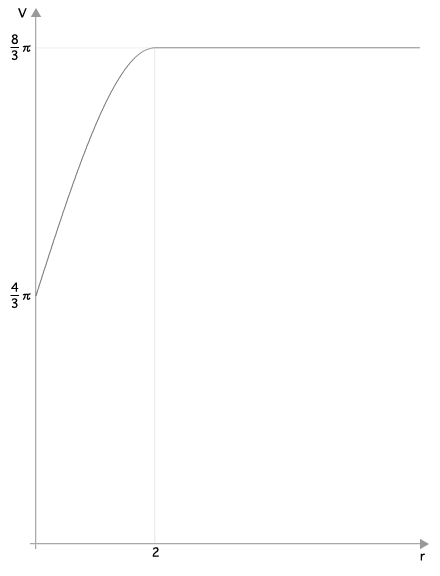
ゆえに(i)〜(iii)によって示された関数Vをグラフで概形で示すと

ここまでのまとめ(感想)
ユークリッドの原論によれば点とは位置を表し部分を持たない(長さや面積、体積などの大きさを持たない)。この場合、(ii)における交点の体積0は単純に成立する。しかし、この立場で設問にある「『点全体よりなる立体』の体積」の意味するところを素朴に幾何学で考えると、その言い回しに違和感を感じる。ただ、現代数学ということで点を単に幾何学的な集合の元のこととみなすのであれば、(ii)においてその概念を示さないと解答として曖昧かも知れないので、とりあえず極限値を使ってみた。
微積の考えが成り立つことを示す一般的な解説では例えば「限りなく0に近い数」といった言い回し(極限値という表現)が出てくるが、幾何学でいうところの位置として2とか3とかいうのは存在(現実のものとして表現)し得ず、実際には限りなく2に近い数、3に近い数を単に記号上、2とか3と表記するととらえたほうが日常の生活レベルでの実感がしやすいのではないだろうか。例えば、グラフ用紙にxy軸を作り、x=2の線を引くと鉛筆なりボールペンなりの芯の太さという誤差が出てしまう。どんなに細い芯を使おうともこれは避けられないけれど、しかし、細ければ細いほど真に近付き、どこまでも限りなく真に近付くことは概念としては可能ではある。つまりxyで表される面においてx=2で表される集合はどんなにルーペやコピーなどで拡大して見ても線が太くならない極細線という立場で数字というものを理解することが求積法を直感で理解する（実感する）する早道であると言えそうだ。
(2) V=8になるとき,rの値はいくらか。四捨五入して小数第1位まで求めよ。
(1)の(i)および(ii)に関して
8
3
π >
8
3
×3.14 >8
であることから

これは、r≧2ではV=8を満たしようがないことを言っています。
V=8となるrは(1)の(iii)で示された0<r<2にただ1つ存在する。

これは(1)の(iii)にある導関数からV=8になるrはひとつしかないことを示しています。つまり、以降を含め、(2)を解くためには結局(1)のような手順を踏む必要があるわけで、(1)は(2)を解くためのヒントとして与えられた設問だと言えそうです。
π ( -
r 3
12
+r+
4
3
) =8
よりrの値を求める。
-r 3
+12r=
96
π
-16

これは両辺に12を掛けたり定数を右辺に追いやったりして式を見やすくしているのですが、この式を見て感じるのは、右辺のπをその近似値3.14で置き換えて計算すれば、左辺のrもある程度の見当は付きそうだということです。
そして、設問の「四捨五入して小数第1位まで求めよ」とか「円周率πは3.14<π<3.15を満たす」といった条件でさらにrの値を絞り込めそうです。
というわけで、そういう方針でやってみることにします。
3.14<π<3.15により、
14.47<
96
π
-16 <14.58

といった感じで右辺は単純な割り算と引き算でおおよそこれくらいの数字であることが分かります。
で、左辺ですが、試しにもっとも計算が楽そうな1をrに代入してみると(-1+12)で11となり14.47よりも小さいことが分かります。なので、(1)の(iii)にあった導関数によりrはもっと大きな値でなければなりません。
この段階で、rは設問により小数第1位までの概数で示すことになっているので1.0〜2.0のいずれかであることが分かります。でも、実際のrの値が1.95以上2.0未満で答えが2.0というのは(1)の(i)および(ii)から考えてあまり気分のよいことではないので、おそらく1.0〜1.9でしょう。
いずれにせよ総当たりで行けそうですが、とりあえず、1と2の中間である1.5くらいで計算してみます。
r=1.5のとき、
-r 3
+12r=14.625

14.58より大きくなってしまいましたが、かなり惜しいところです。なので、今度は1.4で計算してみます。
r=1.4のとき、
-r 3
+12r=14.056

これもまたかなり惜しいですが、今度は14.47より小さくなってしまいました。
ということはrは1.4より大きく1.5より小さい数となりますが、rの値は四捨五入して小数第1位まで求めよとあるので、1.4か1.5のどちらかが答えになります。
なので、1.45未満か以上かで答えが分かることになります。
こんなひねりのない解法で良いのかという気もしますが、因数分解などのいかにもといった感じの関数の解の求めかたは無理そうに思えるのでこのまま突っ走ります。
r=1.45のとき、
-r 3
+12r=14.351375

この数字は14.47より小さいのでrは1.45よりおおきく1.5より小さい数となります。つまり、実際のrの値はともかく、四捨五入した小数第1位までの概数としてはいずれにせよ1.5ということになります。どうやらこれが答えのようです。
なお、もう少し詳しく調べてみるとrは1.487付近です(πも近似値なのでアテになりませんが)。
以上により、四捨五入して小数第1位まで求める場合のrの値は1.5である。

まとめ（感想）
設問を読んだ時点では、あるいは(1)を解き終わるまでは、(2)について、こんな解きかたをすることになるとはなかなか想像出来ないと思います。(1)は普通っぽい微積の問題なので公式さえ知っていれば自信を持って解いて行けそうですが、もしこの(1)がなかったら(2)はかなりの難問になってしまうのではないでしょうか。
いずれにせよ解答する上で積分が関係すると想像が付きますが(2)の問題はいわゆる受験数学の公式的なものを使って解いたわけではありません。
解答のように順序よく考えていけば難しくはないのでしょうが、受験会場の限られた時間のなかでもし(1)がなかったとしたら(その分の点数が与えられないのなら)途中まで解いて分からなくなったときの時間のロスを気にしてこの問題は後回しにしたくなりそうです。
（注意）
この解答はおおよそ当たっていると思いますが、正解であるかどうか、また正確性については保証しません。